ARTIKEL2 - VEKTOREN

von SumFuka

Mathematik - Wuuaaahhh! Ob du es mögen wirst oder nicht, aber es ist sehr wichtig, dass du die hier genannten Sachen verstehst! Jedes mal, wenn du eine Rakete abfeuerst, brauchst du einen Vektor. Jedesmal, wenn sich irgendetwas bewegt, brauchst du Vektoren.

WAS IST EIN VEKTOR?
In einer dreidimensionalen Welt wie Quake besteht ein Vektor einfach aus drei Zahlen: einer x-Komponente, einer y-Komponente und einer z-Komponente. In q_shared.h sehen wir folgende Definition:

Falls du noch nicht so erfahren mit C bist, die typdef-Anweisung verknüpft einen komplizierten Datentyp mit einem anderen. Die erste Zeile definiert, dass ein einfach dimensionaler Vektortyp, vec_t, einfach eine Gleitkommazahl sein soll (also z.B: 23.4567, im Gegensatz zu 23). Die nächsten typedef's definieren 2, 3, 4 und 5 dimensionale Vektortypen. Der am häufigsten gebrauchte ist ein 3D Vektor, vec3_t. Er besteht einfach aus einem Array (Feld) von drei vec_t's (einfacher gesagt, einem Feld von drei floats). Diese drei floats repräsentieren das, was wir x-, y-, und z-Komponente nennen.

DER URSPRUNG
Ok, der einfachste Vektor ist der Ursprungsvektor. Diesen schreibt man in Koordiantenform so: (0.0, 0.0, 0.0). Die x-, y- und z-Komponenten sind alle 0. Laß uns diesen in C nachbauen:

Nun laß uns einen Vektor basteln, der die Position des player0 bei (55.0, -23.0, 12.5) darstellt:

Also, wo steht unser player0 nun? Nunja, das ist abhängig vom...

KOORDINATENSYSTEM
Laß uns annehmen, unser Quake Level ist dreidimensional (und mehrfach übereinander geschichtet). Zum Beispiel eine Spacemap. Laß uns weiter annehmen, der Ort (0.0, 0.0, 0.0) ist genau über einer Plattform, die irgendwo mitten in der Karte ist, die sich links und rechts, vorne und hinten, nach oben und nach unten ein wenig ausdehnt. Aber was ist "links, rechts, vorne, hinten, oben, unten"?

Quake benutzt das sogenannte "linkshändige 3D Koordiantensystem". Das bedeuted, du nimmst deine linke Hand, und zeigst damit nach vorne. Laß deinen Daumen nach oben zeigen, deinen Zeigefinger nach vorne (also von dir weg) und den Mittelfinger nach rechts. Laß uns annehmen, wir stehen direkt im Ursprung der Space Map, und schauen in Richtung Norden.

In dem Fall zeigt dein Mittelfinger in die Richtung der positiven x-Achse, dein Zeigefinger zeigt auf die positive y Achse, und dein Daumen zeigt auf die positive Z-Achse.

Zurück zum Beispiel der Position von player0. Wir sehen nun, der player0 steht rechts von uns (x=55.0 ist positiv), hinter uns (y= -23.0 ist negativ) und über uns (z=12.5 ist positiv).

Wenn wir unseren player0 also spontan nach 64 Einheiten Ost, und 64 Einheiten nach oben teleportieren wollen, wie können wir das tun? Das geht z.B. so:

Doch dafür gibt es einen noch viel besseren Weg...

GESCHWINDIGKEITSVEKTOREN
Alle Vektoren, mit denen wir bisher gearbeitet haben waren Positionsvektoren - also eine (x,y,z) Position irgendwo in der Spiele-Welt. Es gibt aber noch eine andere Verwendung für Vektoren - die Darstellung der Geschwindigkeit (velocity). Wie beschreiben wir die Geschwindigkeit einer Rakete, die 45 Grad nach oben, mit 900 Einheiten pro Sekunde fliegt? Mit einem Vektor!

Das mag ein wenig verwirrend sein, nachdem die Rakete eine Position und eine Geschwindigkeit hat, beide dargestellt durch vec3_t.

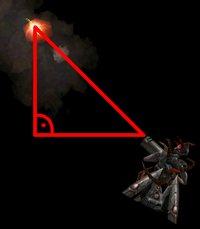
Das Ergebnis: Nach einer Sekunde befindet sich unsere Rakete bei (636.39, 0, 636.39). Aber warum haben wir 636.39 benutzt, und nicht 900? Nun, die Antwort ist einfach. Wir bewegen uns hier ja im zweidimensionalen (sowohl x als auch y Richtung der Rakete ändert sich). Daher ist der gesamt zurückgelegte Wert (900) die längste Seite in dem Dreieck, während die kürzeren beiden jeweils den Unterschied in der jeweiligen Dimension angeben (in unserem Fall 636.39). Hier kommt der gute alte Pythagoras mit a^2 + b^2 = c^2 zu Gute. Also wenn a und b die Werte 636.39 haben... dann hat C 900. Bei dreidimensionalen Bewegungen wird das Ganze noch ein Stück komplizierter...

RICHTUNGEN
Anstatt sich darüber Sorgen zu machen 636.39 aus 900 auszurechnen, gibt es einen besseren Weg um mit der Geschwindigkeit 900 Einheiten pro Sekunde und 45 Grad nach oben gerichtet zu arbeiten. Wir teilen es einfach in zwei Komponenten - die Richtung und die Geschwindigkeit.

Ein Richtungsvektor ist ein Vektor in eine bestimmte Richtung, mit genau der Länge 1.0. Zum Beispiel (1.0, 0.0, 0.0) oder (0.707, 0.0, -0.707) usw.. Wir werden jeden Vektor mit genau der Länge 1.0 als Normalenvektor bezeichnen.

Geschwindigkeit (speed) ist eine lineare Angabe (KEIN Vektor!). Zum Beispiel 900.0, 0.0 oder -450.0.Eine Geschwindigkeit von 0.0 stellt Stillstand dar, wogegen negative Geschwindigkeit Rückwärtsbewegung darstellt.

Was ist einfacher? Nun, es gibt eine einfache Formel die es uns erlaubt Entities durch die Welt zu bewegen: enpos = startpos + speed * direction. Zum Beispiel können wir damit unsere Rakete bewegen:

Aber wieso ist das einfacher? Quake unterstützt uns mit verschiedenen Richtungsvektoren im Code. Wir entdecken z.B. öftes den "forward" Vektor. Dieser zeigt immer gneau in die Richtung, in die wir schauen, und damit zielen. Also, was tun um eine Rakete abzufeuern? Wir nehmen eine Geschwindigkeit (velocity) und multiplizieren diese mit 900. Um eine Railgun abzufeuern, verfolge den Strahl ausgehend vom forward Vektor (also der Blickrichtung, in die man gesehen hat, als man den Feuerknopf gedrückt hat) um 8192 Einheiten. John Carmack hat uns zudem eine mini-library auf den Weg gegeben für die ...

VEKTOR FUNKTIONEN
Nachdem Vektoren so häufig in Quake benutzt werden ist es durchaus sinnvoll für die Veränderungen dieser (kopiern, addieren, mutliplizieren...) Funktionen zu definieren. Nicht nur, dass es eine gute Übung ist diese Funktionen zu benutzen (insbesondere nachdem sie schon da sind), sondern es ist auch wichtig sich darüber klar zu werden, das die Standardoperatioren +, * usw. NICHT benutzt werden dürfen! Denn vec3_t ist ein Feld, und der standardmäßige mathematische Operator kann in C nicht auf ein Feld benutzt werden (zumindest nicht so, wie man es erwarten würde). Als Beispiel:

Hier ist eine vollständige Liste der Funktionen (siehe q_shared.h):

Alles verstanden? Ist dir aufgefallen, dass die meisten Funktionen ein, zwei oder drei Parameter entgegennehmen, um sie dann im zweiten, dritten oder vierten Parameter zu speichern [Ausnahmen sind VectorClear() und VektorSet()]? Der Aufruf VectorSubtract(a,b,c) wird weder a noch b verändern - das Ergebnis wird einfach in c gespeichert. [Die Ausnahme wäre es, wenn wir VectorSubtract(a,b,a) aufrufen würden]

VectorMA(v,s,b,o)
Du hast dich vielleicht schon gefragt, was diese Funktion soll. Es ist eine sinnvolle Kombination von Vektormultiplikation und Vektoraddition. Sie wird sehr häufig benutzt, daher ist es wichtig zu verstehen, was sie tut. Gehen wir zurück zu unserem Raketen-Beispiel...

Dir fällt sicherlich auf, dass wir genau das Selbe getan haben wie zuvor, nur dieses mal mit weniger als der Hälfte an Codezeilen. Und es ist um einiges schicker, da wir die vordefinierten Vektorfunktionen benutzt haben. VectorMA() ist wirklich brauchbar - mach dich mit ihr vertraut... als ob es deine Freundin wäre...intim vertraut... :o)

ALLES MITEINANDER KOMBINIEREN
Ok, wollen wir nun das erlernte in Aktion betrachten. Öffne g_missile.c und such nach folgender Stelle:

Zuerst nehmen wir an, dass "start" die Position ist, von der aus die Rakete abgefeuert wird (also knapp vor dem Spieler). Und "dir" ist die Richtung, in die der Spieler schaut. Also macht dieses Codestück einfach folgendes:

Kopiere den Startvektor in die Untervariable trBase der Struktur bolt

Multipliziere den Richtungsvektor "dir" mit 900 und speichere in trDelta

Konvertiere die Werte von trDelta von Gleitkommazahlen in Ganzzahlen

Kopiere den Startvektor in die Untervariable currentOrigin (aktueller Urpsrung) der Struktur bolt

Das ist auch schon alles, was man tun muß. Schau dir noch ein paar andere Funktionen wie fire_plasma und weapon_railgun_fire an. Versuche herauszufinden wie schnell sich das Plasma bewegt. Was ist die Reichweite der Railgun? Oder der Lightning Gun?

Wenn du all diese Fragen beantworten kannst: Gratuliere, du bist wirklich begabt im Umgang mit Vektoren!

<< zurück/back >>